In this post, I’ll try to explain an alternative route to the famous Einstein Field Equations (EFE) through the principle of least action. All our fundamental theories of physics are described by action principles and gravity is no different. The action principle in general is a relatively simple yet powerful prescription to derive the equations of motion, which in our case will be the Einstein Field Equations. Further it gives an insight to the broad field of variational calculus and some rather technical manipulations which are used in many different areas - therefore, every physicist should know them.

At the end of this – hopefully – rather short blog post you should have gotten an idea of how general relativity can be derived from the Lagrangian formalism and how this gives us a basis to discover new attempts to study general relativity in an alternative way.

Before we get started, huge thanks to my followers on Twitter. I originally tried this on Twitter as a micro blog, but it is rather complicated to explain such an equation-loaded topic within 120 characters. However, I’ve gotten very good and supportive feedback and I’m convinced I can help some people to get a compact and simple but yet unadulterated understanding of this topic. The original post can be found here.

Introduction

The most dangerous black holes, accelerating galaxies and waves of pure gravitation hide behind a plain and simple action. The Einstein-Hilbert action in general relativity is the the gravitational part that yields the Einstein Equations in vacuum through the principle of least action. This is sometimes referred to as the Lagrangian formulation of general relativity. Here I will just quote the EH-action in a aesthetic and coordinate-free version.

It’s very impressive how innocent this equation looks, but it harbors incredible secrets which are still being explored and researched to this day.

\mathcal{S}_{E H}=\frac{1}{2 \kappa} \int_{\mathcal{M}} \star\; \mathcal{R}

The exact form of this action will no longer be interesting here, as we as physicists are often interested in concrete results and therefore have to choose coordinates.

But why exactly does the action have this form?

The Einstein-Hilbert Action

The argument is very simple. Integrating over a manifold $\mathcal{M}$ needs a volume-form. Happily, the metric provides a canonical volume form, which we can then multiply by any scalar function. Our dynamical variable is now the metric $g_{\alpha \beta}$ . Since we know that the metric can be set equal to its canonical form and its first derivatives set to zero at any one point, any nontrivial scalar must involve at least second derivatives of the metric. The Riemann tensor is of course made from second derivatives of the metric, and from general relativity we know that the only independent scalar we could construct from the Riemann tensor is the Ricci scalar $\mathcal{R}$ . Further it is true, that any nontrivial tensor made from products of the metric and its first and second derivatives can be expressed in terms of the metric and the Riemann tensor. Therefore, the only independent scalar constructed from the metric, which is no higher than second order in its derivatives, is the Ricci scalar.

This was first proposed by David Hilbert in 1915.

There is also a nice paper about how Hilbert has found the Einstein Equations before Einstein and some forgeries of Hilbert’s page proofs.

Thus, the Einstein-Hilbert action is given as

\begin{aligned} \mathcal{S}_{EH}=\int_{\mathbb{R}^{D}}\mathcal{L}\;d^{D} x = \int_{\mathbb{R}^{D}} \mathcal{R}\sqrt{-g}\;d^{D} x \end{aligned}

where $D$ is the dimension of our Lorentzian manifold. Further, I used the common notation $g \equiv \operatorname{det}(g_{\alpha \beta})$ for the determinant of the metric tensor. Recall that the Ricci tensor takes the schematic form $R \sim \partial \Gamma + \Gamma^{2}$ while the Levi-Civita connection itself is $\Gamma \sim \partial g$ . This means that the Einstein-Hilbert action is second order in derivatives, just like most other actions we consider in physics.

Deriving the EFE in Vacuum

Let us now vary the action and then require that $\delta \mathcal{S}_{EH}=0$ .

\begin{aligned} \delta \mathcal{S}_{EH}&= \delta \int \mathcal{R}\;\sqrt{-g}\;d^D x \int d^{D} x\; \delta\left(g^{\mu \nu} R_{\mu \nu}\sqrt{-g}\right) \\\\ &=\int d^{D} x \left[\left(\delta g^{\mu \nu}\right)R_{\mu \nu}\sqrt{-g}+g^{\mu \nu}\left(\delta R_{\mu \nu} \right)\sqrt{-g}+g^{\mu \nu}R_{\mu \nu}\;\delta \sqrt{-g}\right] \\\\ &=\int d^{D} x \left[R_{\mu \nu}\sqrt{-g}\;\delta g^{\mu \nu}+g^{\mu \nu}\sqrt{-g}\;\delta R_{\mu \nu} +g^{\mu \nu}R_{\mu \nu}\;\delta \sqrt{-g}\right] \end{aligned}

For the next step we will use a fancy identity, which relates the determinant to the trace of any complex square matrix $\operatorname{M}$ .

\operatorname{det}(e^{\operatorname{M}})= e^{\operatorname{Tr}(\operatorname{M})}

Derivation

First we notice that,

\begin{aligned} \operatorname{M}&=\begin{pmatrix} m_1 & 0 \\ 0 & m_2 \end{pmatrix}\\\\ &\therefore\; \operatorname{Tr}(\operatorname{M})=m_1+m_2 \implies e^{\operatorname{Tr}(\operatorname{M})}=e^{m_1+m_2} \end{aligned}

In a second step we can verify that,

\begin{aligned} e^{\operatorname{M}}&=\begin{pmatrix} e^{m_1} & 0 \\ 0 & e^{m_2} \end{pmatrix}\\\\ &\therefore \; \operatorname{det}(e^{\operatorname{M}})=e^{m_1}e^{m_2}=e^{m_1+m_2} \end{aligned}

Combining these two results we recognize that

\operatorname{det}(e^{M})=e^{\operatorname{Tr}(M)}

With the help of the last equation we can now show, that

\delta \sqrt{-g}=\frac{1}{2} \sqrt{-g}\;g^{\alpha \beta}\delta g_{\alpha \beta}

Derivation

Notice that if we choose $e^{\operatorname{M}}\equiv B$ ( or equivalently $\ln{e^{\operatorname{M}}}=\ln{B}$ ) it implies that $\operatorname{M}=\ln{B}$ . Thus, by using our found identity we get

\operatorname{det}(e^{\operatorname{M}})= \operatorname{det}(e^{\ln{B}})=e^{\operatorname{Tr(\ln{B})}}

So it follows that,

\ln({\operatorname{det}(B)})=\operatorname{Tr}(\ln{B})

If we take now the derivative on both sides we conclude,

\frac{1}{\operatorname{det}(B)}\partial \operatorname{det}(B)= \operatorname{Tr}(B^{-1}\partial B)

This result is remarkable, because setting $B\equiv g_{\mu \nu}\; (\text{and } B^{-1}\equiv g^{\mu \nu})$ finally yields

\delta \sqrt{-g}=\frac{1}{2} \sqrt{-g}\;g^{\alpha \beta}\delta g_{\alpha \beta}

Back to the action we have

\begin{aligned} \delta \mathcal{S}_{EH}&=\int d^{D} x \left[R_{\mu \nu}\sqrt{-g}\;\delta g^{\mu \nu}+g^{\mu \nu}\sqrt{-g}\;\delta R_{\mu \nu} +g^{\mu \nu}R_{\mu \nu}\;\delta \sqrt{-g}\right]\\\\ &=\int d^{D} x \left[R_{\mu \nu}\sqrt{-g}\;\delta g^{\mu \nu}+g^{\mu \nu}\sqrt{-g}\;\delta R_{\mu \nu} +\frac{1}{2}g^{\mu \nu}R_{\mu \nu}\;\;\sqrt{-g}\;g^{\alpha \beta}\delta g_{\alpha \beta}\right]\\\\ &=\underbrace{\int d^{D} x \left\{\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} \mathcal{R}\right) \delta g^{\mu \nu} \sqrt{-g}\right\}}_{\delta \mathcal{S}_{1}}+\underbrace{\int d^{D} x\bigg\{g^{\mu \nu}\left(\delta R_{\mu \nu}\right)\sqrt{-g}\bigg\}}_{\delta \mathcal{S}_{2}} \end{aligned}

Let’s now look at the first term $\delta \mathcal{S}_{1}$ .

Since $\delta g^{\mu \nu}$ is arbitrary, the condition $\delta \mathcal{S}_{1} = 0$ yields that

R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} \mathcal{R}=0

which are the Einstein Field Equations in vacuum.

The Boundary Term

Now we could think that we are finished, since we found the desired equations but we forgot to take care of the $\delta \mathcal{S}_{2}$ term.

For that purpose let’s first look at the Riemann tensor

R^{\alpha}_{\mu \sigma \nu} = \partial_{\sigma}\Gamma^{\alpha}_{\mu \nu}-\partial_{\nu}\Gamma^{\alpha}_{\mu \sigma}+ \Gamma^{\alpha}_{\sigma \gamma} \Gamma^{\gamma}_{\mu \nu}-\Gamma^{\alpha}_{\nu \gamma} \Gamma^{\gamma}_{\mu \sigma}

and the Ricci tensor

R_{\mu \nu}=R^{\alpha}_{\mu \alpha \nu} = \partial_{\sigma}\Gamma^{\alpha}_{\mu \nu}-\partial_{\nu}\Gamma^{\alpha}_{\mu \alpha}+ \Gamma^{\alpha}_{\alpha \gamma} \Gamma^{\gamma}_{\mu \nu}-\Gamma^{\alpha}_{\nu \gamma} \Gamma^{\gamma}_{\mu \alpha}

Varying the Ricci tensor yields

\begin{aligned} \delta R_{\mu \nu} &= \partial_{\sigma}\delta \Gamma^{\alpha}_{\mu \nu}-\partial_{\nu}\delta\Gamma^{\alpha}_{\mu \alpha}\\\\ &+ (\delta\Gamma^{\alpha}_{\alpha \gamma}) \Gamma^{\gamma}_{\mu \nu}-(\delta\Gamma^{\alpha}_{\nu \gamma}) \Gamma^{\gamma}_{\mu \alpha}\\\\ &+ \Gamma^{\alpha}_{\alpha \gamma} \delta\Gamma^{\gamma}_{\mu \nu}-\Gamma^{\alpha}_{\nu \gamma} \delta\Gamma^{\gamma}_{\mu \alpha} \end{aligned}

This looks like the difference between two covariant derivatives.

The covariant derivative is given as

\nabla_{\alpha}(\delta \Gamma^{\alpha}_{\mu \nu})= \partial_{\alpha}(\delta\Gamma^{\alpha}_{\mu \nu}) + \Gamma^{\alpha}_{\alpha \gamma}\delta \Gamma^{\gamma}_{\mu \nu}-\delta \Gamma^{\alpha}_{\nu \gamma}\Gamma^{\gamma}_{\mu \alpha} - \delta\Gamma^{\alpha}_{\mu \gamma}\Gamma^{\gamma}_{\nu \alpha}

\nabla_{\nu}(\delta \Gamma^{\alpha}_{\mu \alpha})= \partial_{\nu}(\delta\Gamma^{\alpha}_{\mu \alpha}) + \Gamma^{\alpha}_{\nu \gamma}\delta \Gamma^{\gamma}_{\mu \alpha}-\delta \Gamma^{\alpha}_{\alpha \gamma}\Gamma^{\gamma}_{\mu \nu} - \delta\Gamma^{\alpha}_{\mu \gamma}\Gamma^{\gamma}_{\nu \alpha}

From that follows

\nabla_{\alpha}(\delta \Gamma^{\alpha}_{\mu \nu})-\nabla_{\nu}(\delta \Gamma^{\alpha}_{\mu \alpha})=\delta R_{\mu \nu}

This equation is also known as the Palatini Equation.

Now, coming back to $\delta \mathcal{S}_{2}$ :

\begin{aligned} \delta \mathcal{S}_{2}&=\int d^{D} x\bigg\{g^{\mu \nu}\left(\delta R_{\mu \nu}\right)\sqrt{-g}\bigg\}=\int d^{D} x\bigg\{g^{\mu \nu}\nabla_{\alpha}(\delta \Gamma^{\alpha}_{\mu \nu})-\nabla_{\nu}(\delta \Gamma^{\alpha}_{\mu \alpha})\sqrt{-g}\bigg\}\\\\ &= \int d^{D} x\; \sqrt{-g} \left(\nabla_{\alpha}\left(g^{\mu \nu} \delta \Gamma_{\mu \nu}^{\alpha}\right)-\nabla_{\alpha}\left(g^{\mu \alpha} \delta \Gamma_{\mu \nu}^{\nu}\right)\right)\\\\ &= \int d^{D} x\; \sqrt{-g} \;\nabla_{\alpha}\underbrace{\left(g^{\mu \nu} \delta \Gamma_{\mu \nu}^{\alpha}-g^{\mu \alpha} \delta \Gamma_{\mu \nu}^{\nu}\right)}_{\equiv A^{\alpha}}\\\\ &= \int d^{D} x\; \sqrt{-g}\;\nabla_{\alpha} A^{\alpha} \end{aligned}

which can be converted to a surface integral by the divergence theorem, which vanishes because the variations are assumed to vanish on the surface $\partial\R^{D}$ .

\mathcal{S}_{EH}=\int d^{D} x \left\{\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} \mathcal{R}\right) \delta g^{\mu \nu} \sqrt{-g}\right\}+\underbrace{ \int d^{D} x\; \sqrt{-g}\;\nabla_{\alpha} A^{\alpha} }_{\text{Boundary term}\; \rightarrow\; 0}

However, there is a small sublety regarding the boundary term. The use of the Einstein–Hilbert action is appropriate only when the underlying spacetime manifold $\mathcal{M}$ is closed (compact and without boundary). If $\mathcal{M}$ has a boundary, the action should be supplemented by a boundary term so that the variational principle is well-defined. This additional term is the so-called Gibbons–Hawking–York boundary term.

Adding Matter

After deriving the famous Einstein Field Equations from $\mathcal{S}_{EH}$ we are now interested in a full action of gravity (if we now consider a spacetime that is not empty). Thus, we have to couple the EH-action with matter fields. This requires some additional terms.

The action of general relativity containing matter is given as

\mathcal{S}_{\text {Gravity}}[g]=\kappa\;\mathcal{S}_{E H}[g]+\mathcal{S}_{\text {Matter}}[g]

Now we have to vary this action again and set $\delta\mathcal{S}_{Gravity}$ = 0. The constant $\kappa$ will be chosen so that we get the right Newtonian limit.

We recall

\begin{aligned} \delta S_{E H}&=\int\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \;\delta g^{\mu \nu} d^{D} x=\int \frac{\delta S_{E H}}{\delta g^{\mu \nu}} \delta g^{\mu \nu} d^{D} x \\\\ &\Rightarrow \frac{\delta S_{E H}}{\delta g^{\mu \nu}}=\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right) \sqrt{-g} \\\\ &\Rightarrow \frac{1}{\sqrt{-g}} \frac{\delta S_{E H}}{\delta g^{\mu \nu}}=R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R \end{aligned}

so varying the whole action gives:

\frac{1}{\sqrt{-g}} \frac{\delta S}{\delta g^{\mu \nu}}=\frac{1}{\sqrt{-g}} \frac{\kappa \delta S_{E H}}{\delta g^{\mu \nu}}+\frac{1}{\sqrt{-g}} \frac{\delta S_{M}}{\delta g^{\mu \nu}}=\kappa\left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right)+\frac{1}{\sqrt{-g}} \frac{\delta S_{M}}{\delta g^{\mu \nu}}=0

Rearranging gives

\begin{aligned} \kappa \left(R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R\right)&=-\frac{1}{\sqrt{-g}} \frac{\delta S_{M}}{\delta g^{\mu \nu}}\\\\ R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R&=-\frac{1}{\kappa \sqrt{-g}} \frac{\delta S_{M}}{\delta g^{\mu \nu}} \end{aligned}

Defining the energy momentum tensor $T_{\mu v}$ as

T_{\mu \nu}=-2 \frac{1}{\sqrt{-g}} \frac{\delta S_{M}}{\delta g^{\mu \nu}}

and doing the substitution with $\kappa=c^{4} / 2(8 \pi G)$ leads to the familiar Einstein Equation which relates the spacetime curvature on the left hand side to the matter energy density on the right hand side

R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} R=\frac{8 \pi G}{c^{4}} T_{\mu \nu}

Adding a Famous Constant

To be honest I lied a little bit by saying that the Ricci scalar is the simplest we could choose. There is in fact a simpler term which we could add to the action (resulting in not interesting dynamics). This comes from multiplying the volume form by a constant.

When the cosmological constant $\Lambda$ is included we have:

\mathcal{S}_{\text{Gravity}}[g]=\kappa\;\mathcal{S}_{E H}[g]+\mathcal{S}_{\Lambda}[g]+\mathcal{S}_{\text {Matter}}[g]=\int d^{D} x \left[ \kappa\;(\mathcal{R}-2\Lambda)\right]+\mathcal{S}_M

So we finally found

R_{\mu \nu}-\frac{1}{2} g_{\mu \nu} \mathcal{R} + g_{\mu \nu}\Lambda=\frac{8 \pi G}{c^{4}} T_{\mu \nu}

Higher Derivative Terms

We have seen that the Einstein-Hilbert action (with cosmological constant) is the simplest thing we can write down to find the EFE but it is not the only possibility, at least if we allow for higher derivative terms. To give an example, there are three terms (the so-called Gauss–Bonnet term) that contain four derivatives of the metric. This modification of the Einstein–Hilbert action is sometimes referred to as Einstein–Gauss–Bonnet gravity.

S_{\mathcal{G}}=\int d^{D} x \sqrt{-g}\;\mathcal{G}=\int d^{D} x \sqrt{-g}\left(a R^{2}+b R_{\mu \nu} R^{\mu \nu}+ c R_{\mu \nu \rho \sigma} R^{\mu \nu \rho \sigma}\right)

with $a, b$ and $c$ dimensionless constants and $\mathcal{G}$ the Gaus-Bonnet term. General choices of these constants will result in higher order equations of motion which do not have a well-defined initial value problem.

Nonetheless, it turns out that one can find certain combinations of these terms, which conspire to keep the equations of motion second order. This is known as Lovelock’s theorem.

Theorem (Lovelock’s Theorem): The only second-order, local gravitational field equations derivable from an action containing solely the $4D$ metric tensor (plus related tensors) are the Einstein Field Equations with a cosmological constant.

This powerful theorem means that if we try to create any gravitational theory in a four-dimensional Riemannian space from an action principle involving the metric tensor and its derivatives only, then the only field equations that are second order or less are Einstein’s equations and/or a cosmological constant. This does not, however, imply that the Einstein-Hilbert action is the only action constructed from $g_{\mu \nu}$ that results in the Einstein Equations. In fact, in four dimensions or less one finds that the most general of such actions is

\mathcal{L}=\alpha \sqrt{-g} R-2 \Lambda \sqrt{-g}+\beta \epsilon^{\mu \nu \rho \lambda} R_{\mu \nu}^{\alpha \beta} R_{\alpha \beta \rho \lambda}+\gamma \sqrt{-g}\left(R^{2}-4 R_{\nu}^{\mu} R_{\mu}^{\nu}+R_{\rho \lambda}^{\mu \nu} R_{\mu \nu}^{\rho \lambda}\right)

The third term vanishes in all dimensions, while the Gaus-Bonnet term is only nontrivial in $4+1D$ or greater, and as such, only applies to extra dimensional models. In $3+1D$ , it reduces to a topological surface term (In lower dimensions, it identically vanishes). This follows from the generalized Gauss–Bonnet theorem on a $4D$ manifold $D=4$ dimensions, this combination has a rather special topological property: a generalization of the Gauss-Bonnet theorem states that

\frac{1}{8 \pi^{2}} \int_{M} d^{4} x \sqrt{g}\left(R^{2}-4 R_{\mu \nu} R^{\mu \nu}+R_{\mu \nu \rho \sigma} R^{\mu \nu \rho \sigma}\right)=\chi(M)

where $\chi(M) \in \mathbb{Z}$ is the Euler character of $M$ .

As in any field theory, higher derivative terms in the action only become relevant for fast varying fields. In General Relativity, they are unimportant for all observed physical phenomena and we will not discuss them further in this course.

Modified Gravity

As an outlook I would like to to give an overview of this space of alternatives to general relativities that has been constructed and injected into the literature over the past $17$ or $18$ years.

So this is the round table of modified gravity theories.

While building a modified gravity theory, Lovelock tells us that if we want a gravity theory that is not general relativity we have to brake one of the clauses implicit in the theorem. It further means that we have only five options if we want to modify the Einstein Field Equations. Lets now run through the five options or categories of theories with a cartoon example of an action.

Theorem (Lovelock’s Theorem): The only second order, local gravitational field equations derivable from an action containing solely the $4D$ metric tensor (plus related tensors) are the Einstein Field Equations with a cosmological constant.

New Field Content

A: Add other fields rather than the metric tensor (e.g. scalar-tensor theories like the Brans-Dicke theory):

S_{\mathrm{Grav}}\sim \int \sqrt{-g} d^{4} x\left[\phi R-\frac{\omega(\phi)}{\phi}(\nabla \phi)^{2}-2 V(\phi)\right]

This first option adds new field content and couples it to the Einstein-Hilbert action and is involved in mediating gravitational forces. One can add scalar fields, vector fields, tensor fields or even mixtures of the previous ones. The action above shows an example of a scalar-tensor theory with an scalar field $\phi$ , with a kinetic term controlled by the function $\omega$ . Further, we have a potential $V$ and we could cook up a potential that gives a universe that accelerate at late times - a dark-energy-like candidate.

Higher Dimensions

B: Use more or less than four spacetime dimensions (Kaluza Klein theories):

S_{\mathrm{Grav}}\sim\int \sqrt{-g} d^{D} x[\mathcal{R}+\alpha \mathcal{G}]

For this option we build a gravity theory in higher dimensional spacetime and work out what the effective $4D$ theory is. That can be very different from general relativity (brane worlds, brane bending modes…)

> 2nd Order Derivatives

C: Add more than second order derivatives of the metric

S_{\mathrm{Grav}}\int d^{n} x \sqrt{-g}\left(R+\alpha_{1} R^{2}+\alpha_{2} R_{\mu \nu} R^{\mu \nu}+\alpha_{3} g^{\mu \nu} \nabla_{\mu} R \nabla_{\nu} R+\ldots\right)

This one is more of a mathematical trick. The field equations contain greater than second order time derivatives. Generally, higher order theories sell trouble. They suffer from Ostrogradski instability instabilities where the Hamiltonians are unbounded from below and spontaneous vacuum decays. However, there are some special cases, in which higher orders are possible and stable.

Non-Locality

D: Non-locality, e.g. for example the inverse d'Alembertian

S_{\mathrm{Grav}}=\frac{M_{P l}^{2}}{2} \int \sqrt{-g} d^{4} x\left[R+f\left(\frac{1}{\square} R\right)\right.

In this option we would get things like a inverse d’Alembertian – a non local operator. Now, when we say non-local it brings to mind some bad things, too. Violation of causality, superluminality and tachyons. But there are good news. We don’t have to suffer from these sicknesses, because there are conditions to include non-local operators and avoid the kind of pathologies just mentioned.

Emergence

E: Emergence – the idea that the field equations don't come from the action.

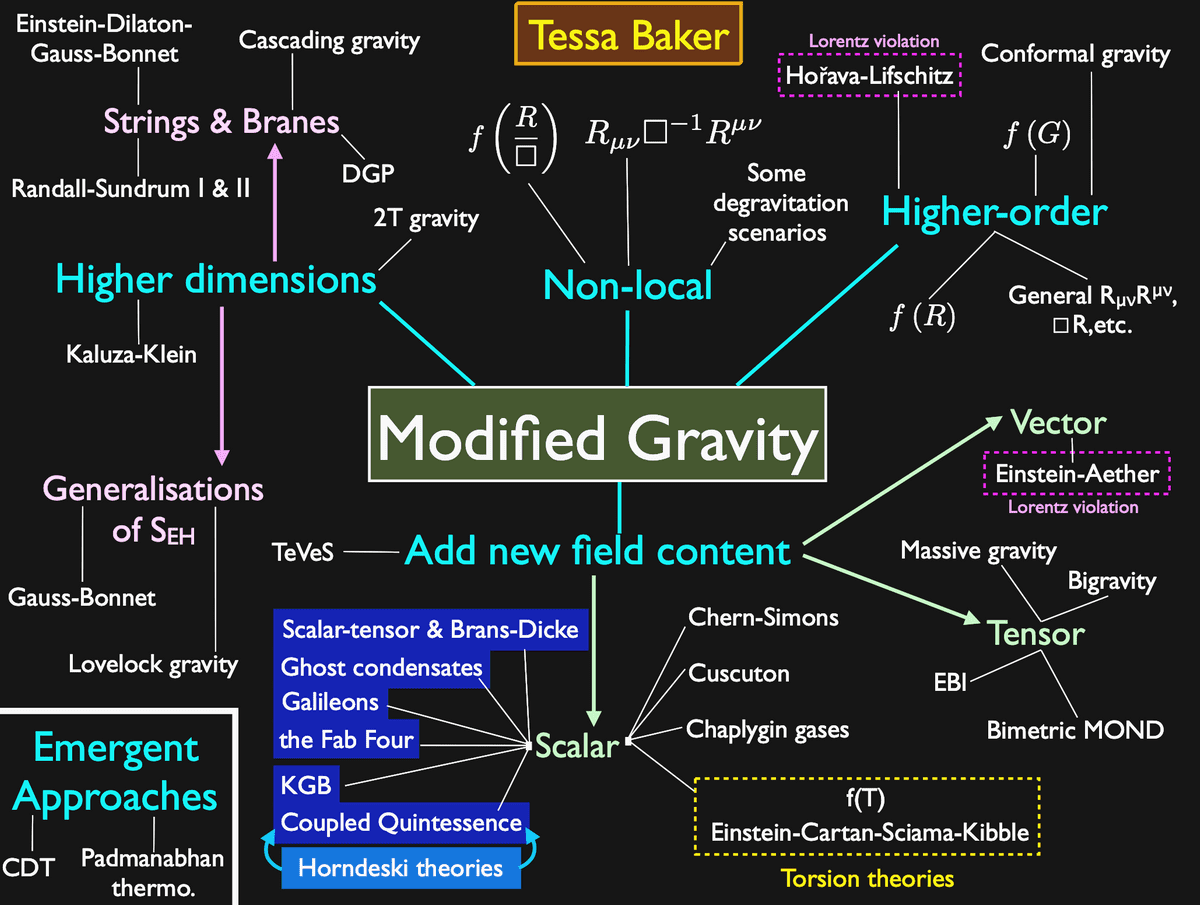
Finally, I would like to show a graphic that Dr. Tessa Baker created. This shows only a fraction of the various alternative branches and theories. This is also a problem because it has become very difficult to classify all theories and many have not yet been tested against experimental data. But that’s a whole different story..

Modified Gravity Modified Gravity – A roadmap. Source: Tessa Baker

If you are interested and want to know more about alternative gravity theory, I recommend this wonderful paper by Timothy Clifton, Pedro G. Ferreira, Antonio Padilla and Constantinos Skordis.

← Previous post

Pages

Blog Posts

General Relativity as a Field Theory