The beauty and importance of light in everyday life are clear to everyone, literally under our eyes. Not surprisingly, then, the same is true also in science, where light has always played a central role. On the one hand, the theory of vision was already studied by the Greek and Roman philosophers, as well as by the Arabs during the Islamic Golden Age. On the other hand, light itself is an excellent tool to study our universe, and its phenomena can be found in most of the investigations carried out in physics. Following the studies of Newton, Faraday and many other pioneers, our understanding was finally consolidated by Maxwell’s landmark works, which laid the foundation of modern optics. More recently, optical systems have become a ubiquitous component for technology, to the extent that it’s hard to overrate their essential contribution. In the wake of this enthusiasm, today light is about to deliver new and even deeper thrills under the magnifying lens of quantum mechanics!

The relevance of quantum mechanics for science - and beyond - is well known, with its counter-intuitive phenomena to deal with and figure out. These curious phenomena have been associated with the so-called first quantum revolution, where scientists tried to unveil the mechanisms hidden behind the new observations. One century has passed since then and we’re now entering the second quantum revolution, where scientists are no longer only spectators of weird phenomena but also use them for practical applications! This long-term vision sets a clear departure from the former, more descriptive approach. Only a few decades later, quantum technologies are now believed to dramatically improve classical approaches in several fields, ranging from the simulation and exploration of complex systems to computer science and communication. All these research areas, which come under the name of quantum information, have recently witnessed great achievements both from the theoretical and experimental side.

This notwithstanding, the stage in which quantum technologies outperform classical devices in relevant problems is still beyond our engineering skills. Indeed, for quantum technologies to tackle problems of practical interest (e.g. factorization), we need many more qubits (the quantum equivalent of the classical bit) and of better quality (less noise, longer coherence time, better connectivity etc.). For this reason, to keep everyone happy and motivated - including funding agencies! - scientists have set an intermediate goal whose relevance, albeit symbolic, has driven an enormous effort on a global scale. This goal consists in finding a problem where a quantum hardware outperforms the best classical counterpart with current technology. This means that it’s not important whether 1. the problem is useful (as long as it’s clear and the comparison is fair!) or 2. the classical algorithm is known to be optimal (i.e. in the future, more efficient algorithms could change the outcome of the challenge!). People refer to this goal as the race towards quantum supremacy or (here) towards quantum advantage. The first demonstration of quantum advantage was reported by Google in 2019 using superconducting qubits. This notwithstanding, we will see how light has played, and is still playing, a prominent role in this quest.

In this blog entry, we will briefly retrace the main steps that lead all the way from Maxwell’s equations to the recent, cutting-edge experiments that seek a photonic quantum advantage. First, we will sketch the derivation of single photons in non-relativistic quantum field theory (with integrals and derivatives for the enthusiasts). Then, we will outline the task that aims to unlock a quantum advantage with near-term technology (for the happiness of computer scientists). Finally, we will sketch recent experiments and the problem of validation (for experimentalists and down-to-earth philosophers). Let’s just make a quick remark before we start: even though qubits are the logical units at the core of quantum information, here we will not need them!

From Classical to Quantum

You have all probably seen the t-shirts with the four Maxwell equations. What if I tell you now that you don’t need 4 equations at all?

In the special theory of relativity we described electromagnetism as a field theory which follows from an action principle (or a so-called Lagrangian density). In the following we will derive the 4 Maxwell equations from an a-priori arbitrary Lagrangian. This will legitimize our principle of action a posteriori. We will then quantize this classical field theory into a so-called quantum field theory, where the “quanta” will be identified with photons.

Maxwell’s Theory from Classical Field Theory

Before we start looking for the quantized photon, a brief reminder about Maxwell’s theory from the point of view of classical field theory.

Let’s start with the Lagrangian density for Maxwell’s equations in the absence of any sources. This is simply

where the field strength is defined by

As you might know, we get the equations of motion by solving the Euler-Lagrange equations. By doing this we get two of the four famous Maxwell equations

Or in terms of $A^{\mu}$:

Okay, but where are the Maxwell equations we know from highschool? To see the equations we need to go from the 4-vector notation to the 3-vector notation. Let’s define $A^{\mu}=(\phi, \vec{A}),$ then the electric field $\vec{E}$ and magnetic field $\vec{B}$ are defined by

which, in terms of $F_{\mu \nu},$ becomes

Using the explicit form of $F_{\mu\nu}$ in the found equations of motion yields two Maxwell equations

The other two Maxwell equations do not result from the action principle. They are more of a geometrical consequence. We can observe that $F_{\mu \nu}$ satisfies the so called Bianchi identity.

Using again our explicit form of $F_{\mu \nu}$ and the Bianchi identity we get the second pair of Maxwell’s equations,

Radiation Field Quantization

We’ve seen, that our classical field theory reproduces electromagnetism. Now let’s quantize. Quantizing is the moment when you have to hand over the cookbook and get creative. The modern approach would of course be the path-integral formalism. But we’re staying old school and quantize canonically, but first things first:

For the quantization procedure we need to compute the the momentum $\pi^{\mu}$ conjugate to $A_{\mu}$

so the momentum $\Pi^{0}$ conjugate to $A_{0}$ vanishes. This means $A_{0}$ is not a dynamical field, while $A_i$ is our old friend, the electric field $E^{i}$.

I’ve been hiding something so far. The Lagrangian has a very large symmetry group, acting on the vector potential as

for any function $\chi(x) .$ We’ll ask only that $\chi(x)$ dies off suitably quickly at spatial $\vec{x} \rightarrow \infty .$ We call this a gauge symmetry. The field strength is invariant under the gauge symmetry:

As always, gauge symmetries spoil that there is a redundancy of the system, therefore we’ll use a gauge. Here we choose the so-called Coulomb or radiation gauge ($\nabla \cdot \vec{A}=0$ and $\Phi=0$). This has the great advantage that the physical degrees of freedom are manifest. However, we’ll lose Lorentz invariance.

In radiation gauge (vector fields satisfying the Coulomb gauge are also called transverse fields) the equations of motions read

which we can solve in the usual way by using plane wave solutions,

with $p_{0}^{2}=|\vec{p}|^{2}$. The constraint $\nabla \cdot \vec{A}=0$ tells us that $\vec{\xi}$ must satisfy

which means that $\vec{\xi}$ is perpendicular to the direction of motion $\vec{p}$. We can pick $\vec{\xi}(\vec{p})$ to be a linear combination of two orthonormal and real vectors $\vec{\epsilon}_{r}$ with $r=1,2,$ each of which satisfies $\vec{\epsilon}_{r}(\vec{p}) \cdot \vec{p}=0$ and

These two vectors correspond to the two polarization states of the photon.

To quantize we turn the Poisson brackets into commutators. Our first guess would probably be

But there is something wrong, because it’s not consistent with the constraints. We still want to have $\nabla \cdot \hat{\vec{A}}=\nabla \cdot \vec{\hat{E}}=0$ imposed on the operators. But then we would get a weird contradiction

What’s going on? In imposing the commutator relations we haven’t correctly taken into account the constraints. Clearly, the fix to this problem is to select the following commutator ¹,

To see that this is now consistent with the constraints, we can rewrite the right-hand side of the commutator in momentum space,

which is now consistent with the constraints, for example

We now write $\hat{\vec{A}}$ in the usual mode expansion,

where, as before, the polarization vectors satisfy

Inserting the mode expansion into the commutator relations will give us the commutation relations for the creation and annihilation operators, which are the usual ones for creation and annihilation operators

where, in deriving this, we need the completeness relation for the polarization vectors,

The Hamilton operator is then (after normal ordering, and playing around with $\vec{\epsilon}_{r}$)

For every ($\vec{p}$, $r$) we can then define a basis states $\lvert n \rangle_{\vec{p}, r}$ that are eigenstates of $H$, with eigenvectors $E_n(\vec{p}) = n \, \hbar \, \omega_{\vec{p}}$. If we then define the number operator $\hat{n}=\sum_{r} \,\int d\vec{p} \; \hat{a}_r^\dagger (\vec{p}) \, \hat{a}_r (\vec{p})$, with $\hat{n} \lvert n \rangle_{\vec{p}, r} =n \lvert n \rangle_{\vec{p}, r}$, we finally arrive to the Fock states $\lvert n \rangle_{\vec{p}, r}$, which satisfy the well-known relations

This suggests that we interpret $\lvert n \rangle_{\vec{p}, r}$ as a state with $n$ particles created by $\hat{a}_{r}^\dagger (\bm{p})$ and destroyed by $\hat{a}_r (\bm{p})$. Photons are born!

Evolution of Fock States

For closed systems, any Hermitian operator $\hat{O}$ evolves under the action of a unitary operator $U(t)$ given by the complex exponentiation of $\mathcal{H}$, i.e. $\hat{O}(t)=U(t) \,\hat{O} \,U^\dagger(t)$. Single-photon wave packet evolution is then described, once again, by the creation and annihilation operators

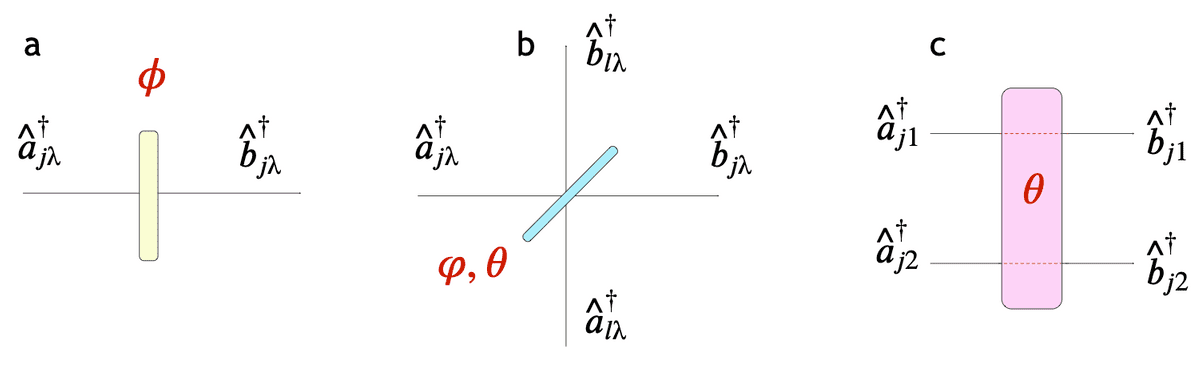
where the wave packet mode function $\alpha_j (\bm{k})$ can be Lorentzian or Gaussian. $U(t)$ can be described using the formalism of Bogoliubov transformations of the mode operators $\hat{a}^\dagger$, whose generators are the interaction Hamiltonians of beam splitters and phase shifters (the most elementary components of linear-optical interferometers) shown in Fig. 1.

Action of the main optical elements in second quantization: phase shifter (a), beam splitter (b) and polarization rotation (c). The indices $j$ and $\lambda$ describe the spatial mode and the polarization, respectively. (Fig. 1)

In this formalism, the most general two-mode interaction that mixes mode operators is given by

with mixing generator $\mathcal{H}\propto\sum_i \hat{c}_i^\dagger \, \hat{c}_i$. Here, for simplicity the indices $(i,j)$ include also the polarization degree of freedom. In the non-mixing case ($\hat a^\dagger \rightarrow \hat a^\dagger$), one finds that

$m$ being the number of optical modes. While this expression can look frightening, there is a very simple way to visualize the physics behind! Here’s the intuition (see also Fig. 2):

• the outer product runs over all optical modes $i$, each with $n_i$ photons.
• the factor in parentheses describes the single-photon evolution: a photon enters mode $i$ and exits in superposition over the $m$ modes. The exponent is there because there are $n_i$ photons in mode $i$!
• the normalization factor $n_i!$ takes care of the $n_i$-particle permutations for the input state.

Next we can derive the scattering amplitude from an input Fock state $\bm{s}=(s_1,...,s_m)$ ($s_i$ is the number of photons in mode $i$) to the output $\bm{t}$

where $U_{S,T}$ is constructed by taking $s_k$ ($t_k$) times the $k$th row (column) of $U$, and

is the permanent of a matrix $(A_{m \times m})_{i j}=a_{i j}$, where the sum is over all permutations $\{\sigma\}$ of $\left[1,..,m\right]$.

A comment for the curious reader: you’re right, the permanent looks just like the determinant (without the sign permutation)! This is due to the particle statistics: the former (latter) describes bosonic (fermionic) evolutions, with states that are symmetric (anti-symmetric) under particle permutations.

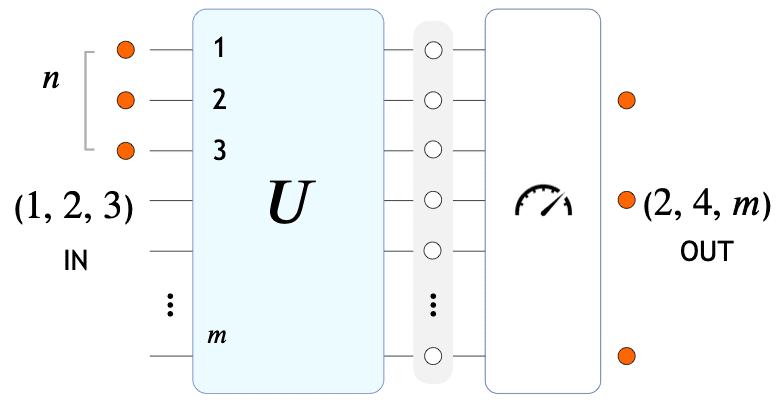
Sketch of a Boson Sampling experiment in the original formulation. From left to right, $n$ photons enter a linear-optical interferometer implementing an $m \times m$ Haar-random unitary transformation $U$. Interestingly, any unitary transformation can be implemented using only phase shifters and beam splitters (see Fig. 1 : a-b). $U$ shuffles the creation operators in such a way that, at the output, photons exit in superposition over all modes. When the output state is measured, photons are found in a random combination of optical modes, which corresponds to sampling from the unknown underlying probability distribution. Here $n=3$, while to show quantum advantage we need $n > 50$ (in the ideal case without losses and partial distinguishability… otherwise things become more complicated!). (Fig. 2)

From single photons to the quest for quantum advantage

So far we discovered that the natural evolution of single photons in a linear optical interferometer is described by the permanent of a certain matrix. Cool… so what? Well, it turns out that this innocent-looking function is extremely hard to evaluate on a computer. Can this fact suggest a way to highlight a separation between quantum and classical systems in terms of, say, performance?

This is precisely the idea behind Boson Sampling, a computational problem introduced by Aaronson and Arkhipov (AA) in 2010 . The task is to sample from the output distribution of an interferometer implementing an $m \times m$ unitary evolution $U$ on an input state with $n$ indistinguishable bosons. While a passive quantum device can efficiently solve this task by evolving single photons (the required physical resources scale polynomially in $m$ and $n$), a classical computer would be confronted with the monstrous computational complexity of the permanent. Computing the permanent is indeed $\#P$-hard (it’s tough even for the simplest 0-1 matrices): the best-known algorithm requires $\mathcal{O}(n\,2^n)$ operations! This hardness was numerically tested in 2016, where it took one hour to the most powerful supercomputer with a matrix of size roughly $50 \times 50$. For an interesting comparison, despite the same number of terms, symmetries in the sign permutation reduce the determinant’s complexity to $\mathcal{O}(n^3)$.

Below we will briefly overview the key points behind the proof of hardness of Boson Sampling. It’s a little bit hard to follow, especially since the author of this post finds it obscure. Still, it’s interesting to retrace the main ideas and connections that made this result possible. If today this is not your priority, you can directly jump to the end of this section and I’ll join you in a moment!

Combining the above observations, Aaronson and Arkhipov finally prove that a classical polynomial-time algorithm for the approximate Boson Sampling would imply the collapse of the entire polynomial hierarchy in computational complexity theory… which is quite unlikely to say the least!

What does this mean? As you may guess, it means that there’s no way for a classical approach, however fast and smart, to solve this problem in an efficient way. For computer scientists and philosophers, this also represents an attack to the extended Church-Turing thesis, which states that “a probabilistic Turing machine can efficiently simulate any realistic model of computation”. Since a quantum device only needs to run the experiment (efficient in the number of photons and modes), Boson Sampling provides a clear route towards a photonic demonstration of quantum advantage!

From Theory to Experimental Demonstration

The ideas presented in the previous section may appear obscure at first sight. Unfortunately, on a second thought they’re actually even more complicated. Yet, we have good news: an actual experiment is easy to describe instead!

Boson Sampling experiments…

The simplest implementation of Boson Sampling can be divided in three main stages (see Fig. 2):

• Generation of $n$ indistinguishable photons. Why indistinguishable? Because if photons were distinguishable, then an $n$-photon experiment would have the same statistics of $n$ experiments with single photons, which is polynomial in $n$ to simulate. Much more complicated (and interesting!) is the case of partial distinguishability and photon losses, for which many recent studies have tried to gauge the trade-off (among all relevant physical quantities) that prevents a classical computer from solving the problem.
• Evolution of $n$ photons in a linear optical interferometer implementing an $m \times m$ ($m>n^2$) unitary transformation $U$ randomly selected according to the Haar measure. Why do we want $U$ to be Haar-random? Well, loosely speaking to avoid simplifications, more specifically to fulfill the assumptions of the problem! n.b. It is very easy to pick a Haar-random $m \times m$ unitary: just use a random unit vector in $\mathcal{C}_m$ for its first row, then a random unit vector orthogonal to the first one for the second row etc.
• Detection of single photons in the output modes. The measured output combinations of Fock states correspond to ampling from the underlying (in general unknown) scattering probability distribution.

Despite its apparent simplicity, requiring no entanglement, adaptive measurements or ancillary systems, its experimental demonstration represents a real challenge for our technological state of the art! The first proof-of-concept experiments, reported in 2013, used $n=3$ photons in up to $m=6$ modes, while a threshold of $n \sim 50$ (or more) indistinguishable photons is now considered to be necessary to claim quantum advantage. Various approaches have been proposed to push its limits, both with photons (with discrete and continuous variables) and other systems such as trapped ions. Photonics probably remains the favorite platform in this race towards quantum advantage via Boson Sampling, especially considering the improvements reported in the last few years. At the time of writing (end of 2020), the world record is set by an experiment with $n=20$ photons (14 detected) in $m=60$ modes … and rumors suggest that the target threshold might already be achieved.

… and the problem of validation

Did you really think that was the end of our quest? Bad news: there’s still one issue to take care of! Is it really that bad, though? In this and the past section we’ve seen the ingredients to achieve quantum advantage via Boson Sampling. What happens, then, when one enters that regime? How can classical people be sure that this is really true?

In the hard-to-simulate regime, where a classical computer cannot (efficiently) simulate a quantum device, the following question becomes crucial: how do we verify its correct operation? The answer to this dilemma involves a new class of classical algorithms that aim to validate the outcomes of a quantum machine. While a full certification is exponentially hard to perform, for complexity reasons similar to the ones presented here, we can make some assumptions to simplify this challenge. A common (non-negligible!) simplification is that experiments are run either with fully distinguishable or fully indistinguishable photons. With this and other assumptions, people have developed a set of validation protocols to accept or reject a Boson Sampling experiment. Ideally, these algorithms should be 1. scalable in the number of photons, 2. sample-efficient (in the lab we only have a finite number of measurements!) and 3. reliable (we would not appreciate a false positive).

The list of validation protocols is rather rich, each with its own strong points and limitations. Here we sketch the ideas behind two of them, which well represent the state of the art in this area:

• Bayesian hypothesis testing: this approach uses Bayesian inference to identify the most likely between the scenarios with fully distinguishable (D) or indistinguishable (I) photons. The intuition is that it’s more likely to measure $n$-photon states from the scenario for which their corresponding probability is higher. This idea is quantified using Bayes’ theorem to update our confidence in each hypothesis. The advantages of this approach are its simplicity and sample-efficiency, the drawback is that it requires the evaluation of permanents, which makes it unfeasible when $n \sim 30$.

• Statistical benchmark: this approach uses statistical features of two-mode correlators in the measured $n$-photon states. These features form clusters in different regions of a suitable space, where each cluster is associated to one of the two scenarios (D, I). By studying what cluster the measured data falls in, and using analytical predictions from random matrix theory, we can cast the validation task as a problem of classification.

Outro

To present the quest for quantum advantage in a compact way, here we had to make a sacrifice and leave out many interesting results. For instance, it would have been nice to add some context on the evolution of optical quantum computing and quantum information, to better appreciate the impact of Boson Sampling. Also, for the sake of brevity we couldn’t present any Boson Sampling experiments, for which we instead refer to a very nice review. Similarly, the role of imperfections would have deserved much more attention, and we could have mentioned relevant studies on the influence of losses and partial distinguishability in Boson Sampling. For a detailed and comprehensive review on these topics, the interested reader can have a look at the following works.

Finally, one last consideration about the journey we just went through. We’ve seen how elegantly light can be described in the classical and quantum framework, and how this is leading us to a demonstration of quantum advantage. This is all fantastic and eye-opening… but is this the end of the story? Well, of course not! While Boson Sampling was designed only to unlock a quantum advantage - with no practical application in mind - it has spurred an entire community to make progress on an unprecedented scale. Remarkable results have been achieved both from the theory side of multiphoton interference and that of the technological platforms. Moreover, Boson Sampling has inspired novel approaches to enhance classical computers with quantum optics. Gaussian Boson Sampling, for instance, can be used to simulate vibronic spectra in molecular dynamics, or to tackle hard problems based on graphs.

Indeed, this certainly doesn’t look like the end of the story, rather like a luminous beginning.

About the Author

Hi! I’m Fulvio Flamini and I’m happy to see you here! Who am I? That’s fun, thanks for asking! During the day, I’m a postdoc in theoretical quantum machine learning, but I was trained as an experimentalist in integrated photonics. At night, I unleash my snail-like creativity writing unfathomable stories or creating a card game for outreach. By the way, when friends joke that I’m good at everything, I just call it being great at nothing :-) One of my aims in life is helping people develop critical thinking and appreciate the wonders of nature. If you know how, or just feel curious about it, you know how to find me.

You can reach me on any of these platforms.

← Previous post

Gravitational Waves - An Invitation