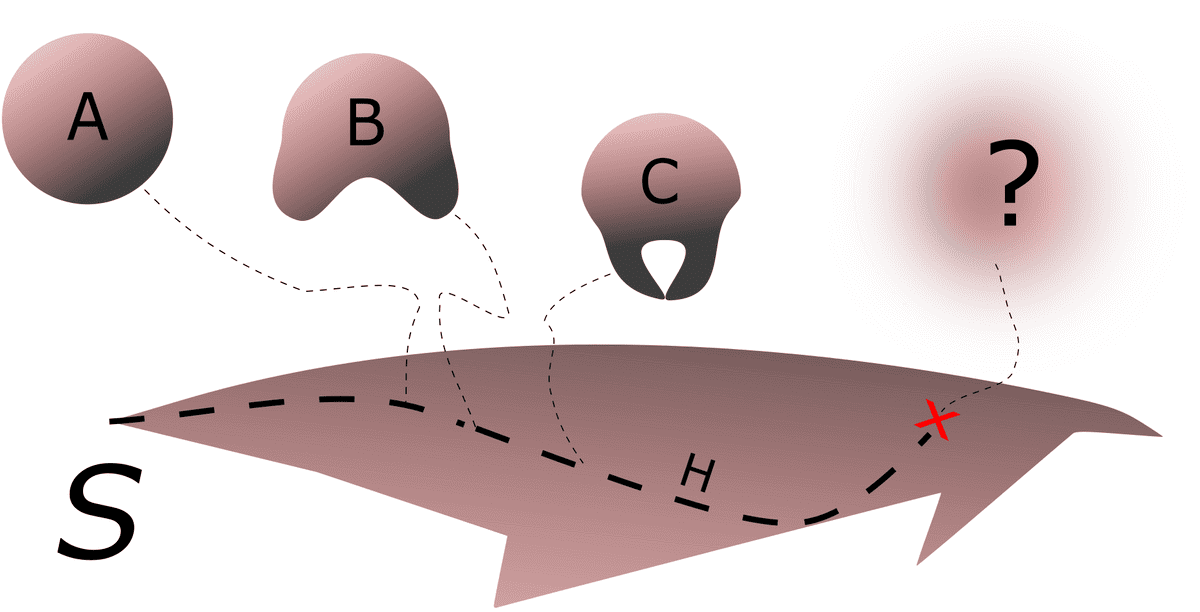Introduction

In 1967 Bryce DeWitt published his famous trilogy on quantum gravity. ”Quantum Theory of Gravity. I. The Canonical Theory” was the title of his first paper discussing the canonical quantization approach of Einstein’s general theory of relativity. He performs the well known Dirac quantization procedure, emphasising in details on the pitfalls he encounters, such as the factor ordering problem and the problem of time. Nevertheless, he triumphs to write an equation that incorporates quantum mechanics and gravity, a Schrödinger-Einstein type of equation, better known today as the Wheeler-DeWitt equation. The equation though was far from complete, and DeWitt was fully aware of this issue. Yet, he carries on attempting to make sense of it. The Wheeler-DeWitt equation is an equation of motion of $\Psi$ , the wave functional of the universe. Upon analysing the geodesics of $\Psi$ , i.e. the possible trajectories the universe can follow, DeWitt realizes a peculiar feature. The universe may ultimately hit a frontier of infinite curvature beyond which it ceases to exist. Is this a physical boundary that our universe will one day reach? Perhaps it is a mere artefact of the equation, or perhaps the Wheeler-DeWitt equation is telling us something about the fate of the universe, like the possible scenario of collapsing into a black hole. Or maybe the Wheeler-DeWitt equation makes no sense to begin with. In any case, the nature of this frontier remains unknown.

This article does not intend to answer this question. DeWitt never disclosed it neither will I attempt to. However, we will take a couple of steps back to the beginning of the story, and grant the reader the freedom to put an end to it.

Once Upon A 3-Geometry

How do you study the evolution of a structure as our universe? Regardless of our humble attempts and our minuscule size compared to this universe that we know no boundary of, to study its evolution is to study the evolution of its geometry throughout time. To be precise, its 3-geometry.

What exactly is a 3-geometry? Let’s start with a simple example, a line. It is a 1-dimensional object. The only thing you can draw on that line is a a set of points which, if you connect, will give you another line. Now take a surface, a 2-dimensional plane. One can draw a set of points equidistant from a center such that, upon connecting the points, we get a circle, a unit-sphere or a 1-sphere. It is a 1-dimensional surface enclosing a 2-dimensional disk. Now go up in dimensions to 3 and take a cube. One can draw a set of points equidistant from a center to obtain a 2-sphere, which is the commonly known term we use for a sphere. It is a 2-dimensional surface enclosing a 3-dimensional 3-ball (In Euclidean space of dimension $n$ , an $n$ -ball is the volume bounded by a surface known as an ( $n-1$ )-sphere). But now what happens if we go up in dimensions another time to 4, and again draw points equidistant from a center. Well, you get a hyper-sphere, a 3-sphere! It is a 3-dimensional surface enclosing a 4-ball.

What does this have to do with the universe? The way to look at it, we live on a 2-dimensional surface (2-sphere) of a 3-dimensional object (3-ball) we call Earth. Now we and the Earth altogether live inside a 3-dimensional object, our universe. Whether this universe is a 3-sphere or not is still an open question, but it is some 3-manifold with some 3-geometry, each of which lead to consequences on the way we view the universe and study its geometrical properties (distances, angles…). Furthermore, whether this 3-manifold is enclosing a 4-dimensional space is irrelevant. What we are interested in is the study of how the 3-geometry of this 3-manifold behave and evolve. An expanded discussion on the shape of the universe can be found here.

A 3-geometry can be studied through its metric tensor $\gamma_{ij}$ , a measure of distances on that 3-manifold. In cosmology, we usually put constraints on how this 3-manifold should be, such as homogeneity and isotropy. The line element is then reduced from 10 to 2 degrees of freedom and can be written as:

\text{d}\Sigma^2=\gamma_{ij}dx^idx^j= a^2(t)\bigg[\text{d}\chi^2+f^2_{\kappa}(\chi)\bigg(\text{d}\theta^2+\text{sin}^2(\theta)\text{d}\phi^2\bigg)\bigg]

When we look at the night sky and observe the universe, what we are really looking at is a snapshot of this 3-geometry which evolves through time. Of course one can argue here that there exists relativistic effects and that the deeper we look at the night sky the older in time we are viewing things, thus our snapshot extends to several 3-geometries. However, cosmologists are fully aware of these effects, and can construct 3-geometries in such a way that we are in a positions of an external observer taking snapshots from the outside. Here we can start to feel the need for the spirit of general relativity, to merge space and time into a 4-dimensional manifold, namely spacetime. Yes, this is a 4-manifold with a 4-geometry expressed through the metric $g_{\mu\nu}$ whose line elements is:

\text{d}s^2=g_{\mu\nu}\text{d}x^{\mu}\text{d}x^{\nu}=-dt^2+d\Sigma^2 \;\;.

The metric tensor $g_{\mu\nu}$ is the solution to Einstein’s field equations:

R_{\mu\nu} -\frac{1}{2}g_{\mu\nu}R + g_{\mu\nu}\Lambda = \frac{8{\pi}G}{c^4}T_{\mu\nu}

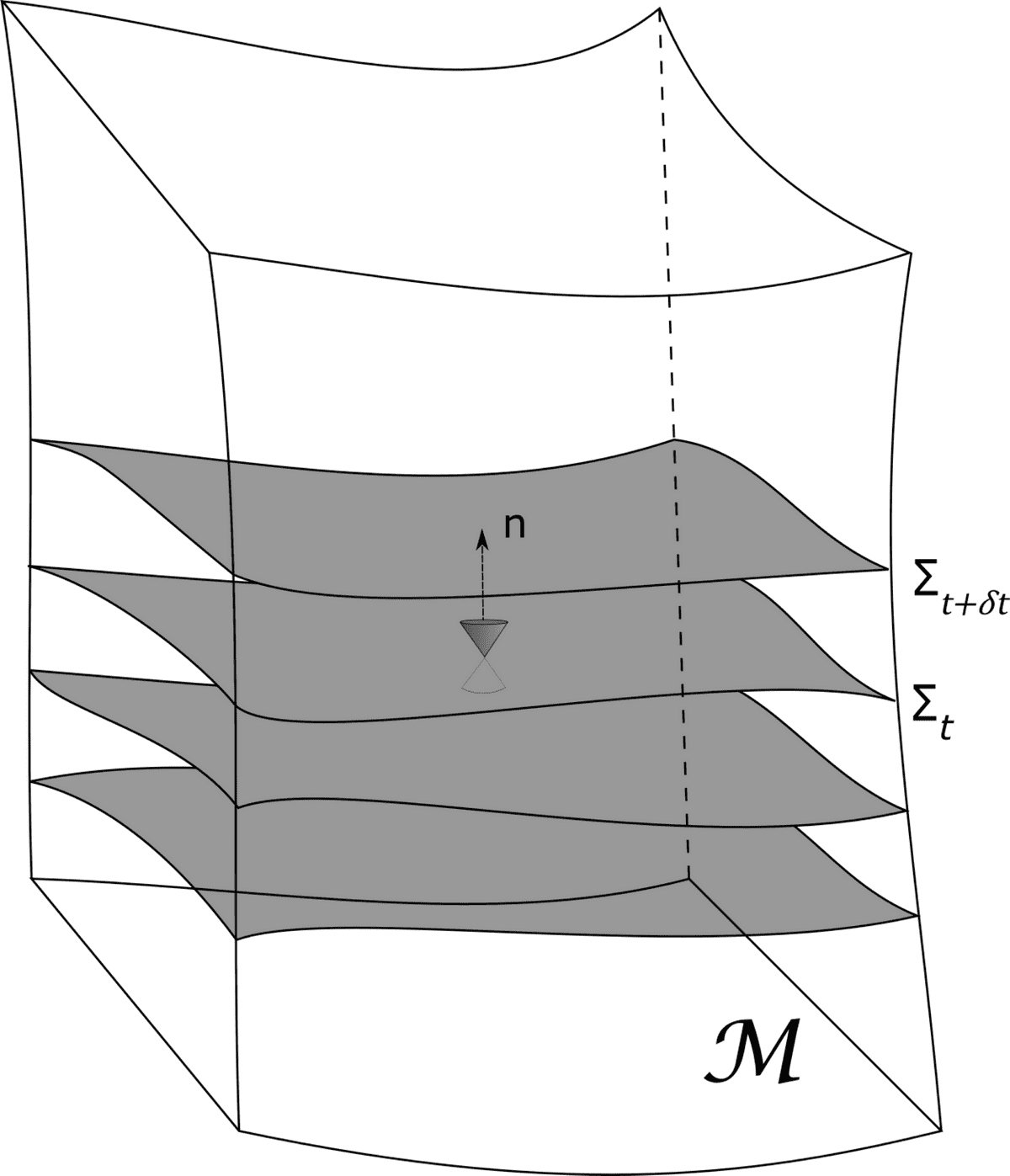
which is there to tell us how space (3-geometry) and time are linked in a region of a given energy and matter content expressed through the Energy-Momentum tensor $T_{\mu\nu}$ . But at the end of the day, when we study the universe and simulate orbits of merging blackholes and neutron stars and exploding supernovae, we break down spacetime into just space, evolving through time. This “breaking down” process is known as the $3+1$ decomposition (see Fig. 1), and it serves to explain the dynamics of the 3-geometry. Therefore, the dynamical object under study here is just space, not spacetime. This is similar as in particle dynamics, where the dynamical object is not $x$ and $t$ , but only $x$ . This is by no means abandoning the notion of spacetime! Spacetime is there, time is a dynamical parameter, but not a dynamical object. After all, this is what Einstein’s general theory of relativity is about, it is a theory of geometrodynamics: of 3-geometry, not 4-geometry.

Foliation 3+1 decomposition of 4-manifold spacetime $\mathcal{M}$ into foliations of spacelike hypersurfaces $\Sigma$ (3-manifolds) (Fig. 1)

The Arena of Geometrodynamics

I hope by now I convinced you that the dynamics of the universe is that of its 3-geometry. This should answer the question posed at the beginning of the last section. This concept will be crucial to understand what follows.

As the universe (the 3-manifold $\Sigma$ ) evolves, so does its 3-geometry which we will label as $^{(3)}\mathfrak{G}$ . It evolves through stretching, bending and curving. We assume that $\Sigma$ does not change its topology. No holes or cuttings are allowed, only diffeomorphisms. This means that at every instant of time, the $\Sigma_t$ is diffeomorphic to $\Sigma_{t-1}$ . One can see that the $^{(3)}\mathfrak{G}$ is an equivalence class of metrics that are transformable, one into another, by diffeomorphisms.

One can track the change of $^{(3)}\mathfrak{G}$ and build some kind of a configuration space where every single point in the space refers to an entire $^{(3)}\mathfrak{G}$ . This space is known as Superspace, and it is our arena of geometrodynamics. The term superspace was coined somewhere in the 1950’s by John A. Wheeler. Superspace can be seen as the “space of all spaces”, specifically Riemannian spaces, and those which are related by a diffeomorphism. Formally the superspace of a 3-manifold $\Sigma$ is the quotient set:

S(\Sigma)= \frac{\text{Riem}\;\Sigma}{\text{Diff}\;\Sigma}\;\;.

Now there are infinitely many spaces $\Sigma$ related by a diffeomorphism, hence the superspace has infinitely many points. Furthermore, there are infinitely many spaces that are not related by a diffeomorphisms, therefore, there are infinitely many superspaces, each of which correspond to a 3-manifold $\Sigma$ . For the time being, we will only consider our universe and its evolution, which makes up a point in one of those superspaces.

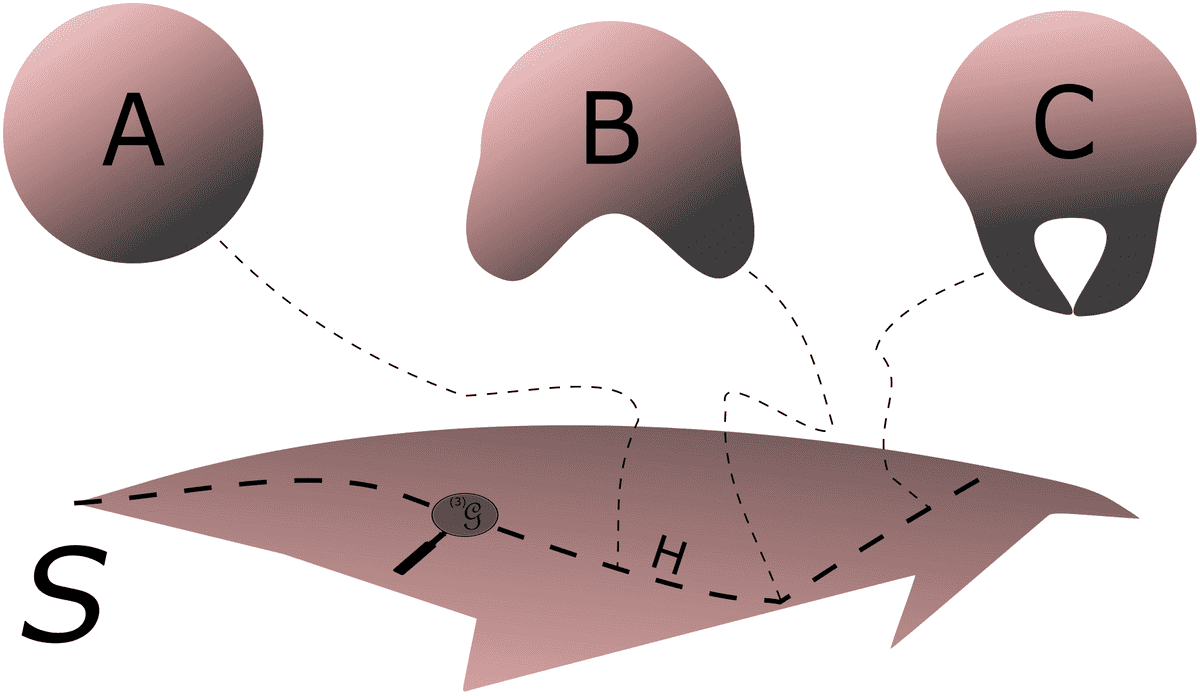
As the universe evolves, it traces a path $\mathcal{H}$ of 3-manifolds ( $\Sigma_t,\Sigma_{t+1},\Sigma_{t+2}...$ ) each of a $^{(3)}\mathfrak{G}$ diffeomorphic to the other (see Fig. 2). Or to put in elegantly:

^{(3)}{}{\mathfrak{G}}(\Sigma_i) \cong^{(3)}\mathfrak{G}(\Sigma_{i+1}) \;\;\;i=0,1,2...

where diffeomorphic is denoted by $\cong$ .

Superspace Superspace $\mathcal{S}$ containing “points” A, B, C… each of which is a 3-geometry diffeomorphic to the other and tracing the path $\mathcal{H}$ . (Remastered artwork; original: J.A. Wheeler.) (Fig. 2)

The word trace is important here, because it gives a notion of time. You see, the spirit of general relativity and spacetime cannot be avoided as we previously claimed. In fact, the path $\mathcal{H}$ is a very familiar object to us, it consists of all those spacelike 3-geometries that can be obtained as spacelike sections through one particular 4-geometry (the 4-geometry of spacetime), that which satisfies Einstein’s classical field equations!

”Time” conceived in these terms means nothing more or less than the location of the $^{(3)}{}{\mathfrak{G}}$ in the $^{(4)}{}{\mathfrak{G}}$ . In this sense “3-geometry is a carrier of information about time”
— J.A.Wheeler

Quantum Geometrodynamics

Wheeler’s ideas of superspace and geometrodynamics did not spring as an alternative way of understanding the behavior of the universe. After all, Einstein’s theory of general relativity served that particular purpose. Wheeler’s main motivation was to go beyond the classical limit, to understand the quantum nature of the universe, quantum geometrodynamics.

Everyone knew back then that general relativity is incomplete. The presence of physical singularities, such as blackholes or the Big Bang, are barriers beyond which we cannot understand. They are a warning sign telling us that our equations no longer work there, and the only way to pass beyond that singularity is by finding an alternative route to what we presently have. General relativity has passed countless tests and predicted phenomena Einstein wrote down 100 years before their discovery. The answer to the problems posed by general relativity do not lie in an alternative description of gravity, the theory works fine in the classical limit. It is in the quantum limit where one needs to rethink about his concept of spacetime. The answer is in a theory of quantum gravity, that which Wheeler hoped to achieve.

To achieve this, Wheeler collaborated with Bryce S. DeWitt, our second protagonist of this story. Their fruitful discussions resulted in a somewhat “Einstein-Schrödinger” equation, a wave equation of $\Psi[^{(3)}\mathfrak{G}]$ , the wave functional of 3-geometries, or loosely speaking the wave functional of the universe. Today this equation is known as the Wheeler-DeWitt equation:

\mathcal{H} \Psi\left[^{(3)} \mathfrak{G}\right]=\left(G_{i j k l} \frac{\delta}{\delta \gamma_{i j}} \frac{\delta}{\delta \gamma_{k l}}+\gamma^{\frac{1}{2}(3)} R\right) \Psi\left[^{(3)} \mathfrak{G}\right]=0

DeWitt extensively analysed this equation. He pointed out its flaws, and frequently called it ”that damn equation”, for it was strange, and full of nasty features. Nevertheless, he was keen in understanding what it meant. One particular aspect DeWitt wanted to understand is the nature of superspace. He was aware that it was a manifold by itself and wrote:

$\mathcal{S}$ ¹ is the domain manifold for the state functional $\Psi$ , and the $^{(3)}\mathfrak{G}$ are its “points.”

Similar to what Wheeler taught us. But he asks the question:

Can one assign a metric, or a pseudo-Riemannian structure, to $\mathcal{S}$ ?

From the Wheeler-DeWitt equation, DeWitt realizes that the object $G_{ijkl}$ can be seen as a contravariant metric of some 6-dimensional Riemannian manifold $M$ . He emphasizes that such an interpretation is inappropriate because $G_{ijkl}$ is part of the operator $\mathcal{H}$ , but is nevertheless useful to study the properties of the manifold it defines. DeWitt was hoping to connect the properties of $M$ to $\mathcal{S}$ .

Now given any metric tensor, one can follow the rules of differential geometry and compute the connection coefficients and the curvature and other properties of the manifold defined by this metric. For $G_{ijkl}$ , DeWitt computed the curvature, now 6-Ricci (equivalent to the 4-Ricci of spacetime):

^{(6)}{}{R}=-\frac{60}{\zeta^2}

Moreover, upon analysing the geodesics in $M$ , i.e. trajectories of free falling particles, he noticed that all geodesics ultimately hit a frontier at $\zeta=0$ . Looking back at the curvature at $\zeta=0$ , we notice the peculiar feature that the curvature $^{(6)}{}{R}$ is infinity! It appears to be that there is some kind of a blockage at $\zeta=0$ , a frontier, beyond which no point in $M$ can go. Does this frontier exist in the superspace $S$ aswell?

DeWitt rewrites the Wheeler-DeWitt equation in another form:

\left[-\frac{\delta^{2}}{\delta \zeta^{2}}+\frac{(32 / 3)}{\zeta^{2}} \bar{G}^{A B} \frac{\delta^{2}}{\delta \zeta^{A} \delta \zeta^{B}}+(3 / 32) \zeta^{2} {}^{(3)}R\right] \times \Psi\left[^{(3)} \mathfrak{G}\right]=0

Here, it clearly shows the presence of a singularity at $\zeta=0$ . But whether the geodesic incompleteness in $\textit{M}$ leads to a geodesic incompleteness in $\mathcal{S}$ is unclear. Could it be that there is a point in superspace beyond which the 3-geometries such as our universe cannot exist? And if so, what does it mean to tell us about the fate of our universe?

“The question at issue is whether the frontier in $\textit{M}$ generates a corresponding barrier in $\mathcal{S}$ beyond which there is no possibility of extending the state functional. Unfortunately, in the present state of our knowledge no clear-cut answer can be given to this question.” — Bryce DeWitt

It seems that the problem of singularities is following us. Wheeler’s hope of a theory of quantum gravity through quantum geometrodynamics was in vain. DeWitt noticed these problems early on and dedicated most of his research to other approaches to quantum gravity that rely on path integral techniques. But then again, the question remains:

“Is the Wheeler-DeWitt equation and the frontier of any meaning?”

Superspace Superspace is a scenario where a frontier, marked with the red cross, is present, blockading the evolution of 3-geometries. (Fig. 3)

References

Quantum Theory of Gravity. I. The Canonical Theory Bryce S. DeWitt Phys. Rev. 160, 1113 - Published 25 August 1967.
Superspace and the Nature of Quantum Geometrodynamics. J.A. Wheeler (Princeton U.) 1968.

About the Author

Hi! My name is Ali Lezeik. I’m a human among a billion other and a mind of many. In this short life span we have, we are constantly fascinated by the beauty of the world, many of which we have explained and even more left unanswered. It is this beauty that gives me a meaning, and probably to many of you. And it is the journey, despite the frustrations, that gives me joy. So who am I? I like to think of myself as those old voyagers who sailed to the unknown, and came back home to tell the world about the treasures they found and the stories they lived. I might not know how to sail the oceans, but I am learning how to sail the abstract world of physics and how it connects to our world. This is my journey, and these are the stories I would like to share with you.

You can reach me on any of these platforms.

In the original paper he uses the letter $\mathfrak{M}$ to denote the superspace.↩

← Previous post

General Relativity as a Field Theory

Pages

Blog Posts

The Last Frontier